| inviato il 22 Marzo 2020 ore 0:28
“ Allora sarà anche chiaro che i due sensori, FF e APSC, avranno la stessa identica gamma dinamica? „
Sì se stampi a dimensioni diverse, con un rapporto pari a quello tra le superfici dei sensori. Ora è chiaro? |
| inviato il 22 Marzo 2020 ore 0:35
Santa pazienza...cerchiamo di metterci un punto.
Allora:
- prendo una fotocamera come la D850, sottoespongo di quattro stop, recupero in PP, ridimensiono il file a 5000px lato lungo chiamandolo FILE A;
- prendo una fotocamera come la D500 (aps-c con la stessa densità della D850, grossomodo) oppure molto più semplicemente, prendo il crop aps-c della stessa D850; sottoespongo di quattro stop, recupero in PP, ridimensiono il file sempre agli stessi 5000px lato lungo chiamandolo FILE B; questo per simulare una stampa delle medesime dimensioni;
- il risultato è che FILE A ha meno rumore di FILE B
CHIARO? E' CHIARO?? 
Uff.... |
| inviato il 22 Marzo 2020 ore 1:31
È da tempo che è invalsa l'abitudine di parlare di "densità" di un sensore. Più o meno è come quelli che chiamano "lente" un obiettivo. In effetti in inglese "lens" indica sia una lente semplice che un obiettivo. In italiano no.
Densità è ancora più fuorviante perché è una quantita intensiva che assume significato solo se si chiarisce a cosa è riferita. Si può definire una densità di un sensore lineare come (numero di pixel)/mm. O superficiale come (numero di pixel)/mm2. Se uno vuole fare il precisino la densità in SI andrebbe riferita rispettivamente a m e m2.
Ma resta il fatto inconfutabile che non esiste una formula o relazione dove si introduca la densità. Perché non ha senso.
Tutta la fotografia digitale è imperniata intorno a tre grandezze: f/ intesa come rapporto (adimensionale) fra lunghezza focale e diametro della apertura. Non importa l'unità di misura. Quando Leitz sul Summicron scriveva 5 cm, allora il diametro dovea essere in cm. Nessuno impedirebbe di usare ancora SI e parlare di m di lunghezza focale, l'importante è che f/ è un numero puro. È anche importante nelle varie formule sostituire a f/1.4 il vero valore che è f/sqrt(2) ossia f/1.41. f/5.6 in realtà è f/5.65685... In altre parole, gli f/ non interi sono troncati alla prima cifra decimale. Se fai i conti con una sola cifra decimale introduci errori abbastanza seri di arrotondamento, specie quando f/ compare al quadrato (come nella EV, per esempio).
f/ è legato alla diffrazione attraverso la lunghezza d'onda lambda. Lambda gli spettrocopisti la indicano in nm nel VIS. Per i nostri scopi torna più semplice indicarla in µm (il volgarissimo micron). Il primo disco di Airy ha diametro 2.44*lambda*f/. La comparsa di lambda è una turbativa importante per i profani che in media sono convinti che ad un certo f/ ci sia sempre la stessa diffrazione. Poi sono persi, hanno bisogno di un numero in µm per identificale lambda. Alcuni usano lambda=0.500 µm, altri lambda=0.520 µm, altri ancora lambda=0.550 µm. Queste tre lunghezze d'onda sono quelle del verde(giallo) G.
Finalmente arriva il nostro pixel, più o meno "denso2 secondo i profani. In realtà nel digitale si parla di pixel pitch, la distanza fra i centri di due pixel (meglio sensel) adiacenti. Fra due pixel ci sta l'isolante. Se l'isolante è sottile rispetto alla dimensione lineare del sensel, allora con ottima approssimazione pixel pitch=~dimensione lineare del sensel.
Se qui intoducete "densità" dei sensel vi attorcigliate in inutili complicazioni di tipo dimensionale.
Se lambda è in µm conviene indicare la dimensione lineare del sensel d in µm.
Questo è importante: un modello sufficiente di quello che succede in fotografia digitale ha solo bisogno di f/, lambda e d. Più precisamente è il rapporto (lambda*f)/d che fa capire se il sistema è "optics limited" o "detector limited" o una miscela di tutti e due.
Siamo arrivati al momento decisivo: quando abbandoniamo una descrizione nello spazio immagine e passiamo alle frequenze spaziali nelle immagini.
Riposto per l'ennesima volta un grafico che in ordinata porta MTF e in ascissa 1/d e 1/(lambda*f/).
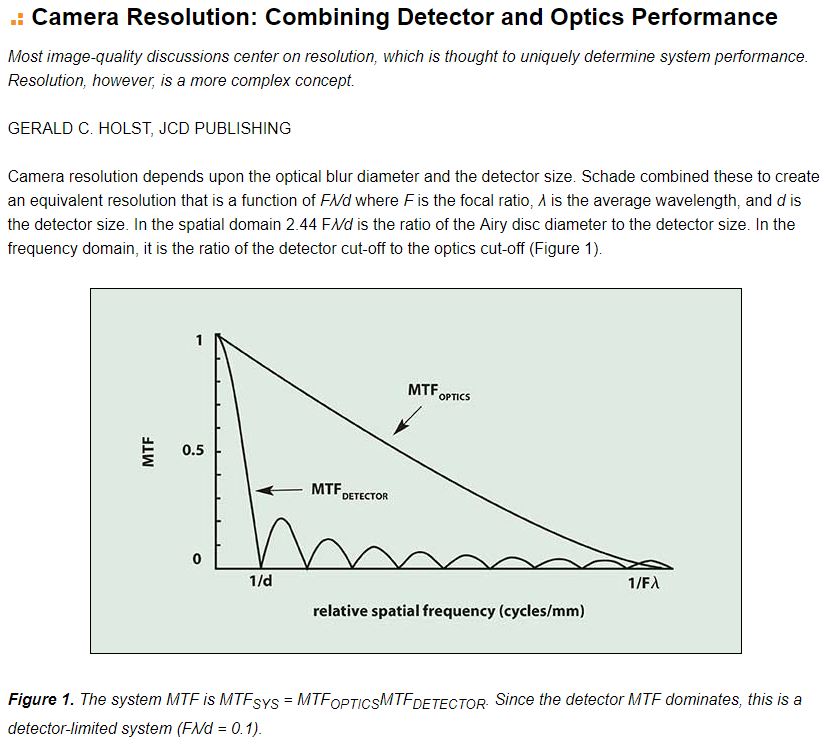
In questo caso (lambda*f/)/d è uguale a 0.1 (se contate i lobi sono proprio 10). In alto c'è un obiettivo "diffraction limited".
In fotografia digitale usiamo soltanto la prima metà del primo lobo a sx, il resto sono spurie (non è vero al 100%, tanto è vero che ci sono gli obiettivi apodizzati).
Inutile illudersi: non capire davvero questo grafico porta a inenarrabili frescacce, di tutti i tipi.
|
| inviato il 22 Marzo 2020 ore 2:58
Quindi per d che tende a 0?  |
| inviato il 22 Marzo 2020 ore 7:31
@Walther ho dovuto mettere il pistolotto per chiarire pochi termini ma chiari. Principalmente per fotografi come te. Però riconosco di averti solo irritato, naturalmente non era il mio scopo e chiedo venia
@Otto d=0 sta per un sensel infinitamente piccolo che poi si tradurrebbe in un numero di pixel tendente all'infinito.
Un sensore ideale così avrebbe MTF100 a qualsiasi lp/mm.
Prima di scappare troppo in avanti ricordiamoci che le MTF sono un modello semplice e utile, ma si riferiscono a situazioni di messa a fuoco perfette e soprattutto di SNR alto (illuminazione ottimizzata delle mire, ad esempio).
Se si esagera coi Mpx, ad un certo punto risolvi quello che vuoi con SNR sempre decrescente, al punto che, come si diceva a Milano, ti attacchi al tram con la iper-risoluzione.
Credo che il senso di questo 3D sia di mettere in luce che una R4 con 61 Mpx è ben lontana dal distruggere la risoluzione con bassi SNR.
A livello personale vorrei sottolineare, se ce ne fosse bisogno, che sono affranto e che più che altro posto pistolotti per non lasciarmi il tempo di piangere |
| inviato il 22 Marzo 2020 ore 9:03
“ @Otto72,
se l'intento era quello di aumentare gli ingredienti del minestrone l'operazione è andata a buon fine, dopo la sottoesposizione di 4 stop e ridimensionamento più recupero in post ora possiamo dedicarci a fare le prove con altri valori in -Ev, poi magari altre in +Ev così vediamo le bruciature e per il 2050 forse ci arriviamo. „
No, ho solamente tentato di spiegare perché se vai su DxO e prendi la suddetta D850, nella misura in crop mode trovi una GD diversa (minore).
Ma evidentemente, non sono stato abbastanza chiaro.  |
| inviato il 22 Marzo 2020 ore 9:43
"Ma alla fine le bigmpx hanno una IQ migliore.."
Quando uno dice "migliore" deve definire anche le condizioni al contorno, altrimenti resta una parola vuota.
Su sensori di tecnologia identica, le bigmpx hanno gli stessi parametri immagine delle pochimpx, la differenza è irrisoria, (Dxo) ed invisibile in uso pratico, e vado poi a definire i"parametri immagine", come la GD, il rumore, la profondità di bits colore e sensibilità ai colori del sensore, e per "bigmpx" fotocamere da 50 - 60 Mpx rispetto a fotocamere da pochimpx, ossia da 21 - 24 Mpx.
Se i parametri immagine sono gli stessi, la Qualità d'Immagine, sul formato geometrico nativo di quelle più piccole, è la stessa, come colore e risoluzione, ma la pochimpx resta con MTF più alte e dunque un capellino più nitida.
Il lato positivo delle bigmpx è che fanno un formato nativo geometrico più grande, a pari PPI di file immagine, rispetto alle pochimpx, e quello l'unico fattore positivo, mentre i lati negativi delle bigmapx rispetto alle pochimpx sono fondamentalmente due, maggior sensibilità al micromosso ed entrata in diffrazione visibile, a pari formato di stampa, su diaframmi un pochino più aperti, il rumore oggi è praticamente uguale tra le due, le bigmpx sono un capellino più rumorose, ma in uso pratico non si vede se non molto raramente.
Ma come MTF di sistema, la pochimpx rsta sempre a valore maggiore
Andare a dire "tout court" che le bigmpx sono migliori come immagine rispetto alle pochimpx è dunque sbagliato se non si definisco i parametri al contorno.
la nitidezza, come prima dimostrato, è sempre e comunque maggiore nelle pochimepx rispetto alle bigmx
Se non hai capito, e può accadere, ti faccio l'esempio di una stampa formato francobollo, 3 x 4 cm, scatta ad F 22 con la stessa ottica: non vedrai mai la differenza di risoluzione tra una bigmpx ed una pochimpx, mentre probabilmente la vedrai, sempre come risoluzione, su una stampa di 120 X 160 cm scattata ad F4.
A monitor, con le dimensioni attuali dei monitor, ma soprattutto con le risoluzioni attuali dei monitor, la differenza di risoluzione non la vedrai mai, è impossibile, mentre la pochimpx sarà un capellino più nitida, ma solo se hai il monitor veramente buono.
Su stampe A3 ed A2, le pochimpx sono tendenzialmente più nitide delle bigmpx, dipende dal tipo di foto.
|
| inviato il 22 Marzo 2020 ore 10:16
“ A livello personale vorrei sottolineare, se ce ne fosse bisogno, che sono affranto e che più che altro posto pistolotti per non lasciarmi il tempo di piangere „
Allora ti do una mano io con qualche domanda.
Applicando il grafico ad un sensore FF di 24MP avrei che il primo lobo della curva MTFsensore andrà a zero per una frequenza di 167 (=1/0.006) cy/mm che corrispondono a 167lp/mm, ed ad una frequenza della metà, 83lp/mm, si avrà il valore di 0.64 (2/Pgreco), giusto?
La frequenza di Nyquist per una 24MP è 83lp/mm oppure 167lp/mm?
Consideriamo il sensore perfetto, senza filtro AA e senza matrice Bayer.
|
user175879 | inviato il 22 Marzo 2020 ore 10:42
“ “ Allora sarà anche chiaro che i due sensori, FF e APSC, avranno la stessa identica gamma dinamica? ?
Sì se stampi a dimensioni diverse, con un rapporto pari a quello tra le superfici dei sensori. Ora è chiaro? „
Otto, l'unica cosa chiara è che non ti è chiaro cosa significa gamma dinamica. La mia impressione è che tu confondi la gamma dinamica con il numero di passaggi tonali che ci sono tra il punto più scuro e quello più chiaro di un'immagine. In realtà la gamma dinamica è un rapporto che tiene conto solo dei valori minimo e massimo possibili e non delle sfumature intermedie, e non vedo come questo possa essere influenzato dal rapporto di ingrandimento della stampa.
Se invece dobbiamo parlare di gradazioni tonali, e non di gamma dinamica, allora è abbastanza ovvio credo che un sensore più grande sia avvantaggiato semplicemente perché a parità di angolo di campo, e quindi di scena ripresa, dispone di un maggior numero di fotositi ed è quindi in grado di riprodurre la stessa scena con un maggior numero di informazioni tonali. Questa sua maggiore definizione tonale risulta viepiù evidente quanto maggiori sono le dimensioni della eventuale stampa. |
| inviato il 22 Marzo 2020 ore 10:58
Beh, già solo questo, servirebbe a capire che più punti ci sono e meglio è. O sbaglio? |
| inviato il 22 Marzo 2020 ore 10:59
“ Otto, l'unica cosa chiara è che non ti è chiaro cosa significa gamma dinamica. La mia impressione è che tu confondi la gamma dinamica con il numero di passaggi tonali che ci sono tra il punto più scuro e quello più chiaro di un'immagine. In realtà la gamma dinamica è un rapporto che tiene conto solo dei valori minimo e massimo possibili e non delle sfumature intermedie, e non vedo come questo possa essere influenzato dal rapporto di ingrandimento della stampa. „
No, a me è chiarissimo, è a te che non è chiaro che per molti ha poco senso parlare di GD se non normalizziamo l'output, ossia la dimensione di stampa e/o di ingrandimento a video. Cerca di fare uno sforzo in più per capire quello che ho scritto sopra: l'esempio è assolutamente calzante.
Questo è il motivo per cui DxO presenta per la gamma dinamica due scale: "screen" che è appunto la misura fatta al livello di pixel - dove le fotocamere con meno mpx, a parità di tecnologia, fanno sempre meglio - e "print" dove appunto l'output è normalizzato a 8mpx, similmente all'esempio che ti ho proposto io, e allora le cose cambiano, ribaltando a volte l'esito del confronto.
Il rumore, che limita l'estensione verso il basso, se ingrandisci di più (cosa che occorre fare con i sensori più piccoli per avere la stessa dimensione di stampa) si vede di più e diventa più importante rispetto al segnale.
Comunque, tornando alla nitidezza, vi propongo questi scatti dal balcone, gli unici che riesco a fare in questo particolare momento:

Dall'alto in basso, da sinistra a destra:
- a9 con Voigt 125 Apo Lanthar, crop 200%
- a7r4 in aps-c mode con 85GM, crop 200%
- a7r4 in FF con Voigt 125 e crop a 24mpx FF equivalente (126%)
- a7r4 con crop 200%
Stessi parametri di sviluppo in C1 per tutte.
|
| inviato il 22 Marzo 2020 ore 11:05
Otto, questo test non lo vedo molto affidabile, nelle due immagini sotto è apparsa una mosca.
Va rifatto.
 |
| inviato il 22 Marzo 2020 ore 11:07
Pignolo  |
| inviato il 22 Marzo 2020 ore 11:14
@Rolu le frequenze spaziali dell'oggetto e dell'immagine sul sensore hanno di mezzo un fattore 2 che è poi Nyquist.
Per 24 Mpx FF possiamo prendere il sensel come 6µm con tutte le semplificazioni al contorno che hai già scritto.
In un mm ci sono 1000 µm (i vil meccanci li chiamano micron!). In 1000 µm ci stanno 1000/6=167 pixel (sensel).
Se fossimo nei domini tempo/frequenza e dovessimo campionare una sinusoide pura, il criterio di Nyquist ci impone di prendere "almeno" due punti per periodo. Nel caso fotografico immagina che righe bianche e nere siano onde quadre che non sono sinusoidi ma hanno un periodo anche loro. Non era scontato, ma Nyquist funziona anche per spazio/frequenze spaziali oltre che per tempo/frequenze. Un periodo sarà partire da una riga nera e arrivare alla prossima riga nera. In mezzo ci sarà una riga bianca. Per il minimo necessario per distinguere righe bianche e nere bisogna che un sensel intercetti una nera e quello adiacente una bianca, quindi due campioni per periodo (ciclo, cycle), ossia Nyquist. Se in un pixel cadono contemporaneamente una riga bianca e una nera non li hai risolti.
Deriva che un sensel da 6 µm ha Nyquist a 167/2=83 lp/mm, come avevi già precalcolato tu.
Per arrivare a MTF64 a Nyquist devi ricorrere alla MTF del sensel che è sin(PI*f)/(PI/f) ossia una sinc.
f vedilo come cicli. La sinc va a 0 per f=1 ciclo perché sinPI=0. Nyquist sta a f=mezzo ciclo=1/2. Hai già fatto tu il calcolo che è MTF=0.63661... abbreviabile in MTF64. (Quando sono eleganti le formule sono quasi poetiche ). Qui c'è di mezzo PI/2 e traiamo una costante universale per qualsiasi sensel a Nyquist: MTF64! ). Qui c'è di mezzo PI/2 e traiamo una costante universale per qualsiasi sensel a Nyquist: MTF64!
Nyquist è il minimo sindacale, il fotografo avveduto cercherà di andare incontro all'ottica che monta abbastanza lontano da Nyquist. Se l'ottica avesse MTF50 a 60 lp/mm (niente di troppo esagerato), il 24 Mpx FF (scordandosi AA e demosaicizzazione che sono ulteriori turbative) restituisce un MTF(sistema)=MTF(0.5*0.8)=MTF40. Se usi l'esagerata R4: MTF(0.5*0.92)=MTF46. Più Mpx ha il sensore meno danneggi la MTF originale dell'obiettivo.
In tutta questa discussione si è assunto che MTF rispecchiasse la "nitidezza". Se la "nitidezza" si intende in modo diverso, non è escluso che queste siano considerazioni sballate.
Insomma: un sensore più Mpx ha e meno abbassa la MTF di un'ottica. Questo non è affatto condiviso da tutti in questo 3D.
E allora avanti con post di esempi reali, io sono uno sperimentale, non un teorico. |
| inviato il 22 Marzo 2020 ore 11:54
Sulla diffrazione, che affliggerebbe le bigmpx più delle altre, anche in questo caso, non è vero ciò vero ma quel che sembra, ovvero che se ragioniamo al 100% è vero, ma se normalizziamo l'output, accade questo:

sinistra a9, destra a7r4, f/22 è un diaframma "abbastanza" chiuso, no?  |
Che cosa ne pensi di questo argomento?Vuoi dire la tua? Per partecipare alla discussione iscriviti a JuzaPhoto, è semplice e gratuito!
Non solo: iscrivendoti potrai creare una tua pagina personale, pubblicare foto, ricevere commenti e sfruttare tutte le funzionalità di JuzaPhoto. Con oltre 257000 iscritti, c'è spazio per tutti, dal principiante al professionista. |

Metti la tua pubblicità su JuzaPhoto (info) |


 JuzaPhoto contiene link affiliati Amazon ed Ebay e riceve una commissione in caso di acquisto attraverso link affiliati.
JuzaPhoto contiene link affiliati Amazon ed Ebay e riceve una commissione in caso di acquisto attraverso link affiliati.