| inviato il 04 Aprile 2020 ore 0:40
Come promesso, questa è la giustificazione del perché la frequenza spaziale "diffraction limited" è in lp/mm e non in linee/mm. cy/mm (cicli/mm o anche periodi/mm) sottintende sempre una coppia di linee lp, non linee singole.
(da Boreman)
|
| inviato il 04 Aprile 2020 ore 8:52
Grazie a Rolubich mi sono finalmente rinsaldato sulle lp/mm .
Adesso è possibile analizzare questa affermazione “ Nitidezza e risoluzione sono in antitesi, se alzi la risoluzione, cala la nitidezza, ed è Fisica, non ci puoi fare nulla, così è, sia sull'ottica (natura del vetro) che sulla Fotocamera (campionamento per la creazione del Pixel) „
È una frase imprecisa che va analizzata. Per il principio di conservazione dell'energia (sic!) che sono in antitesi (meglio: in qualche modo inversamente proporzionali) sono risoluzione e SNR nella fotografia digitale.
Che limita l'ottica non è la "natura del vetro", bensì la diffrazione. È vero però che il limite di f/ è f/0.5. Gloria a Stanley che ha usato uno Zeiss adattato CINE a f/0.70!
"Campionamento per la creazione del Pixel" (meglio: il sensore a base di Si) non influisce sulla "nitidezza" che in questo modo: sensel più piccoli elevano la MTF(sensore) e quindi la MTF sistemica sensore+obiettivo, se poi questa non è la "nitidezza" si discute anche di SNR e micromosso.
A sostegno di queste inesattezze questo grafico di Brandon Dube (AiryDiscus sotto DPR Forum):
Prudenza impone che si postino grafici dopo averli capiti. La traccia rossa descrive un ottica "diffraction limited".
Non è difficile (fissata la lunghezza d'onda a 500 nm come fa sempre Brandon Dube) risalire a che f/ si riferisce partendo da MTF80 a 200 lp/mm: è f/1.57 (cambia se al posto di 500 nm ha usato 550 nm, per cui sarebbe f/1.43).
MTF80 a 200 lp/mm a TA è "diffraction limited", cioè esente da qualsiasi aberrazione.
Il filtro AA è un semplice cos che si calcola partendo dalla intersezione con l'asse x (~ 160 lp/mm in questo caso).
Infine la MTF del sensel è una semplice sinc, che si è già discussa e calcolata precedentemente.
Nyquist è a 100 cy/mm ovvero lp/mm. L'obiettivo a Nyquist è MTF90 a 100 lp/mm, mica male! Peccato che MTF(Nyq) sia MTF64....
Da dove provengono tutte queste idee confuse? Fondamentalmente dai tempi della pellicola.
Questa è l'MTF della mitica Velvia 50
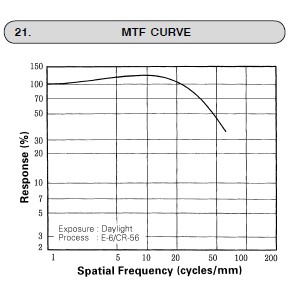
Quello che salta all'occhio è che fino a 20 lp/mm MTF è oltre MTF100, cioè il contrasto è follemente alto! La traccia si ferma a MTF~35 a ~60 lp/mm.
Da queste caratteristiche si deduce che la Velvia, giustamente famosa per contrasto e colori, era un rivelatore meno risolvente dei sensori digitali moderni. Poi sul Forum ci sono affermazioni per cui proiezioni Velvia 2x3 m sono spettacolari. Sicuramente sì, ma a che distanza di visione? Se uno ci va con una loupe, cambia tutto!
|
| inviato il 04 Aprile 2020 ore 11:01
Ah, scusate. Io avevo inteso l/mm come le vecchie lin/mm della pellicola e le Lp/mm come le nuove linee-pixel.
Cioè io intendevo che le vecchie 100 lin/mm corrispondevano alle nuove 200 Lp/mm dei pixel / mm necessari per ottenere le vecchie 100 l/mm. Invece è esattamente il contrario, quindi dobbiamo intendere che le coppie 100 lp/mm corrispondono alle nuove 200 l/mm. Ero io che avevo frainteso, chiedo scusa.
Quindi la mia frase del 02 Aprile 2020 ore 19:23 :
, u , . , uc , , MTF , , dove u e uc sono espressi in l/mm ( uc=286.32 lp/mm )
andrebbe corretta in :
, u , . , uc , , MTF , , dove u e uc sono espressi in lp/mm ( uc=286.32 lp/mm )
e tutti i valori scritti sotto uc andrebbero scritti con uc=286.32 lp/mm, giusto?
cosa faccio, la riscrivo in un prossimo post? |
| inviato il 04 Aprile 2020 ore 12:20
“ Grazie a Rolubich mi sono finalmente rinsaldato sulle lp/mm;-). „
Mi fa piacere non per il fatto di aver ragione, ma per essermi levato un dubbio che avevo perché i miei conti non tornavano con i tuoi; grazie a te che mi hai fatto approfondire questo argomento.
|
| inviato il 04 Aprile 2020 ore 12:35
@Rolu 
@Gio il tuo programma è corretto perché usa il rapporto adimensionale u/u(c), non importa se usi l/mm (doppio) invece di lp/mm. Sbagliavo quando convertivo allo spazio-immagine dividendo per 2, non occorre. Il fattore 2 c'è sempre per calcolare la frequenza di Nyquist. In questo modo tutto è coerente con l'unità di misura lp/mm.
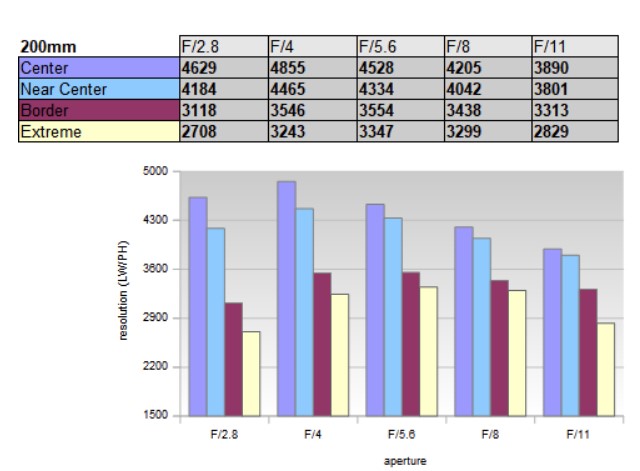
Dove compaiono davvero linee e non coppie di linee (lp) è in MTF come questa di "opticallimits". Non ho trovato il Sony 200-600, questo è il GM 70-200 a 200 mm. Sono riferiti a MTF50. Si leggono come "tot linee contenute nel lato corto (LW/PH)". Se al posto di un FF usi un aps-C hai di mezzo il crop 1.5 e naturalmente il centro è lo stesso mentre i bordi FF non sono giusti, vanno riposizionati.
|
| inviato il 04 Aprile 2020 ore 12:39
Ora ho rifatto i calcoli, ma escono nuovi risultati, potrebbero essere corretti? :
, u , . , uc , , MTF , , dove u e uc sono espressi in lp/mm ( uc=286.32 lp/mm )
50.0 286.3 0.7788
55.0 286.3 0.7569
60.0 286.3 0.7352
70.0 286.3 0.6918
80.0 286.3 0.6489
90.0 286.3 0.6065
100.0 286.3 0.5645
110.0 286.3 0.5232
120.0 286.3 0.4824
130.0 286.3 0.4424
140.0 286.3 0.4032
150.0 286.3 0.3649
160.0 286.3 0.3275
170.0 286.3 0.2912
180.0 286.3 0.2560
190.0 286.3 0.2220
200.0 286.3 0.1895
210.0 286.3 0.1584
220.0 286.3 0.1291
230.0 286.3 0.1016
240.0 286.3 0.0762
250.0 286.3 0.0532
260.0 286.3 0.0330
270.0 286.3 0.0162
280.0 286.3 0.0039
P.S. : ho letto ora il tuo post precedente, i nuovi calcoli sono dovuti al nuovo valore di "u", prima lo dividevo per 2, ora non più... devo studiare...
PROGRAM MTF
CHARACTER*8 FIL4
FIL4="fl46.txt"
OPEN(8,FILE=FIL4)
! PIGRE=2/PIGRECO
PIGRE=0.636619772367
U1=50.0
A1=5.0
UC=286.32
WRITE(8,62)U1,UC
62 FORMAT(1X,2F8.1)
DO 180 N1=1,64
UUC=U1/UC
UUC2=1-UUC**2
IF(UUC2.LE.0.0)GOTO 190
U2=UUC*SQRT(1-UUC**2)
COSM1=ACOS(UUC)
XMTF=PIGRE*(COSM1-U2)
WRITE(8,82)U1,UC,XMTF
82 FORMAT(1X,2F9.1,F10.4)
IF(U1.GT.59.5)A1=10.0
U1=U1+A1
180 CONTINUE
190 CLOSE(8)
STOP
END
|
| inviato il 04 Aprile 2020 ore 12:50
@Gio sei partito da f/6.35 e 550 nm. I calcoli sono perfetti così, ero io che dividevo per 2 sbagliando |
| inviato il 04 Aprile 2020 ore 12:59
Ah OK... Grazie mille ! ho pure aggiunto le altre righe sopra che indicano la tendenza a zero di MTF per valori prossimi a u=286.3 . |
| inviato il 04 Aprile 2020 ore 18:41
Nikon 1 J5, adattatore Nikon FT1, duplicatore Kenko vintage, f/5.6 portato a f/11 dal duplicatore, 1/20s, cavalletto, ISO 160, Tamron VC 70-300 a 300mm, focale equivalente ~ 3650 mm, solito estintore (dietro uno vetrata!) a ~ 40m di distanza, autoscatto 10", PP sotto NX-D.
Per dimostrare che sensel piccoli da 2.37 µm non fanno male alla "nitidezza", che il duplicatore non getta al vento metà risoluzione, che la diffrazione non è invadente, che è meglio fare prove che sentenziare a braccio... Un po' massacrata dal duo Postimage/Juza.
Si è partiti da qui:
|
| inviato il 05 Aprile 2020 ore 16:53
Ferme restando tutte le condizioni di ripresa (è cambiata solo l'ora del giorno), conviene usare un duplicatore mediocre o ritagliare? Qual è meglio secondo il vostro occhio? Teniamo presente che siamo quasi a 4000 mm equivalenti. |
| inviato il 05 Aprile 2020 ore 17:05
Quindi sensel piccolo-sensore da 1 pollice-adattatore-duplicatore-zoom alla massima estensione-ritaglio e ottieni la leggibilità di quei caratteri a 40 metri? Sei un eccellente debunker Valgrassi!  |
| inviato il 05 Aprile 2020 ore 17:47
@Albi il sensorino in realtà è un vantaggio, taglia a 211 lp/mm, è un Sony BSI, fra qualche anno lo stesso sensel lo monteranno sulle FF.
Come tutti gli 1" si siede ad alti ISO, naturalmente. Il duplicatore Kenko è vecchissimo, quelli di oggi hanno più lenti e sono molto meglio. Neanche pensare di andare a mano libera a queste focali equivalenti. Poi viene un punto in cui i caratteri non li leggi perché un ritaglio eccessivo ti ha lasciato troppo pochi pixel. Non riesco a fare questo con i 36 Mpx della A7R, troppo pochi.
I due scatti sopra sono a f/11 per escludere l'effetto della diffrazione. A sx ci sono 4 volte più pixel che a dx.
Il Tamron 70-300 si difende soltanto a 300 mm, ma questo è vero sul formato FF. Qui si usa solo la parte centrale del tele. |
| inviato il 05 Aprile 2020 ore 18:03
Quella di sx sembra leggermente più risolvente.
Ho completato altri calcoli MTF anche per F/4, dalla formula di Valgrassi :
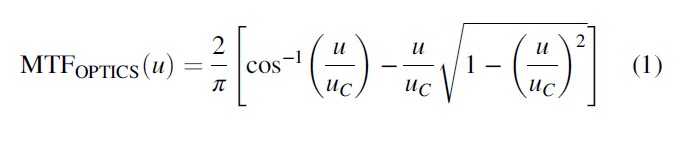
, , u , MTF(F/4) , MTF(F/6.35)
. . 60. 0.8324 . 0.7352
. . 65. 0.8185 . 0.7135
. . 70. 0.8047 . 0.6918
. . 75. 0.7909 . 0.6703
. . 80. 0.7771 . 0.6489
. . 85. 0.7633 . 0.6276
. . 90. 0.7496 . 0.6065
. . 95. 0.7358 . 0.5854
. 100. 0.7222 . 0.5645
. 105. 0.7085 . 0.5438
. 110. 0.6949 . 0.5232
. 115. 0.6813 . 0.5027
. 120. 0.6678 . 0.4824
. 130. 0.6409 . 0.4424
. 140. 0.6141 . 0.4032
. 150. 0.5876 . 0.3649
. 160. 0.5613 . 0.3275
. 170. 0.5352 . 0.2912
. 180. 0.5093 . 0.2560
. 190. 0.4837 . 0.2220
. 200. 0.4584 . 0.1895
. 210. 0.4334 . 0.1584
. 220. 0.4087 . 0.1291
. 230. 0.3844 . 0.1016
. 240. 0.3604 . 0.0762
. 250. 0.3368 . 0.0532
. 260. 0.3136 . 0.0330
. 270. 0.2909 . 0.0162
. 280. 0.2686 . 0.0039
. 290. 0.2468 . 0.0000
. 300. 0.2255 . 0.0000
. 310. 0.2047 . 0.0000
da ulteriori calcoli più fitti , risulta :
il limite dei valori di “u” lp/mm per un obiettivo teorico "diffraction limited" esente da aberrazioni ottiche è :
con diaframma F/4 , con F/6.35
MTF25 , , , , , , 288 , , , , , 182
MTF50 , , , , , , 184 , , , , , 115
quindi per MTF25 il limite è di 288 lp/mm con diaframma F/4 ed invece 182 lp/mm con diaframma F/6.35
invece per MTF50 il limite è di 184 lp/mm con diaframma F/4 ed invece 115 lp/mm con diaframma F/6.35
i calcoli e la conclusione sono corretti ? Grazie |
| inviato il 05 Aprile 2020 ore 23:38
Grazieeeee , allora ho studiato bene ? sono promosso ? Come premio mi regali la tua SHARP ? |
Che cosa ne pensi di questo argomento?Vuoi dire la tua? Per partecipare alla discussione iscriviti a JuzaPhoto, è semplice e gratuito!
Non solo: iscrivendoti potrai creare una tua pagina personale, pubblicare foto, ricevere commenti e sfruttare tutte le funzionalità di JuzaPhoto. Con oltre 251000 iscritti, c'è spazio per tutti, dal principiante al professionista. |
Metti la tua pubblicità su JuzaPhoto (info) |
JuzaPhoto contiene link affiliati Amazon ed Ebay e riceve una commissione in caso di acquisto attraverso link affiliati.
