| inviato il 01 Aprile 2020 ore 16:14
@Bergat il dato più importante riportato è sensel=3.88 µm. Confrontalo col 3.76 µm della Sony A7RIV. Questo è un sensore al top. Essendo X-Trans la possibilità che riscontri Moiré è quasi nulla perché ha Nyquist addirittura a 129 lp/mm! Dovresti montare un obiettivo che risolva 140 lp/mm e contemporaneamente avere una scena con dettagli fitti e ripetitivi (tipicamente: trame di tessuti e tapparelle abbassate da lontano) per avere Moiré. Si elimina con due clic sotto ACR/Brush, raramente è un dramma.
Fuji è nota per proporre obiettivi di classe (gli obiettivi CINE Fujinon sono molto rinomati). Con un sensore così prestante, gli metti davanti qualsiasi Fujinon e sei a posto. Il concetto è che devi prefissarti una risoluzione per te necessaria, metti 40 lp/mm (non è poca..). Vai su Fuji e controlli l'MTF dell'obiettivo. Metti che a 40 lp/mm al centro ti dia MTF50. Col tuo sensore MTF50 lo porti a MTF(0.5*0.96)=MTF48. Ossia hai fatto pochissimo male all'ottica in sé, da MTF50 dell'obiettivo sei arrivato a MTF48 del sistema.
Devi prestare più attenzione quando monti obiettivi vintage non Fuji. Vanno quasi sempre bene, ma ci possono essere casi in cui un sensore così capace di risolvere fa del "male" a un obiettivo veramente modesto. Con sotto mano un MTF reale sarebbe tutto più semplice da spiegare |
| inviato il 01 Aprile 2020 ore 16:51
Grazie Valerio per la spiegazione. Uso solo obiettivi nativi, pur avendo obiettivi nikon e quelli dell'hasselblad (40 distagon 80 planar e 180 sonnar), ma dovrei usarli in MF e complice l'età non è una cosa che faccio volentieri. |
| inviato il 01 Aprile 2020 ore 18:03
Penso che "u" sia la risoluzione alla quale vuoi calcolare il valore MTF e "uc" la risoluzione limite.
Questa formula però è valida per lenti ideali, per trovare la MTF del sistema hai bisogno della MTF dell'obiettivo reale che non la calcoli, si può misurare o prendere le curve MTF a disposizione.
|
| inviato il 01 Aprile 2020 ore 18:09
Ok, grazie, ho capito pure la
MTF(A7R2)=MTF(0.50*0.88)=MTF44 :
era una semplice 0.50*0.88=0.44, è passato del tempo ed ho dimenticato molte cose...
Rimane da capire lo 0.88 da dove è stato ricavato.
Ah, forse il risultato viene dalla formula MTFoptics impostando "u" e "uc" . Sto studiando... so che poi Valgrassi mi darà un brutto voto ( 5--) . |
| inviato il 01 Aprile 2020 ore 18:31
0.88 è il valore MTF di un sensore FF da 42MP ad una frequenza di 60lp/mm (frequenza che è stata fissata per fare il confronto), è un valore teorico ricavabile da una formula.
|
| inviato il 01 Aprile 2020 ore 18:44
“ Ah, forse il risultato viene dalla formula MTFoptics impostando "u" e "uc" . Sto studiando... so che poi Valgrassi mi darà un brutto voto ( 5--) MrGreen . „
Intanto ti bacchetto io .....e poi magari Vlagrassi bacchetta me 
Quella formula riguarda esclusivamente l'ottica, non c'entra il sensore.
Il valore 0.88 si ricava così:
e' più comodo trovare il parametro
(PIgreco * frequenza) / (2 * Ny) = 0.8568
dove:
Ny = frequenza di Nyquist = 110lp/mm per una 42MP FF
frequenza = 60lp/mm (fissata a priori)
MTF sensore = sin(parametro)/parametro = sin(0.8568)/0.8568 = 0.882
NB: impostare la calcolatrice in radianti
|
| inviato il 01 Aprile 2020 ore 22:29
@Rolu grazie per non farmi sentire un mona solitario!
@Gio al famoso 0.88 ci si arriva arrivo attraverso la sinc, cioè la FT del sensel. La sinc formalmente è sen(x)/x. Però il Papa delle Trasformate di Fourier applicate (Bracewell) ha proposto sinc=sin(PI*x)/(Pi*x) per il semplice motivo che PI è il periodo di questa funzione (è un po' come i matematici che indicano l'unità immaginaria con "i" e gli ingegneri elettrici che usano al suo posto "j", per loro "i" è la corrente!). PI naturalmente è pi greco (Juza mi restituisce il simbolo come pi greco maiuscolo, non minuscolo). Quando x=0 è il famoso limite =1 di scolastica memoria. Quando x=PI, sinc va a 0. Nyquist è semplicemente sinc(PI/2) ossia 2/PI=0.6366. Si conclude: a Nyquist qualsiasi MTF è MTF64.
x=1 è un intero ciclo (periodo) e x=1/2 è mezzo ciclo (Nyquist). Schematizzando le righe bianche e nere come onde quadre, un pixel per soddisfare il criterio di Nyquist deve descrivere al massimo mezzo ciclo, cioè un'onda quadra o il vuoto fra le onde quadre, il bianco o il nero (il bianco non assorbe e riflette tutte le lunghezze d'onda della luce, il nero al contrario le assorbe tutte, questo in teoria, in pratica anche il bianco e il nero di un ColorChecker qualcosa si lasciano scappare). Nello spazio oggetto si parla di l/mm, appena si arriva al sensore come spazio immagine si parla di lp/mm per via di Nyquist.
Nessuno trova intuitive le frazioni di periodo. Una volta che si usano lp/mm in maniera consistente (ossia: tutte le volte che si parla delle frequenze spaziali nello spazio sensore) è più semplice dalla dimensione d del sensore risalire a Nyquist con:
1000(µm/mm)/(2*d(µm)). Per esempio 42 Mpx danno 1000/(2*4.51µm)=~111lp/mm. Il 2 è per Nyquist.
Per arrivare al famoso 0.88 in corrispondenza di 60 lp/mm, si fa: sen(PI*60/111)/(60/111*PI)=0.8841...
La relazione che dà la MTF di un apertura circolare (quindi è l'ottica ideale e la diffrazione, il sensore non c'entra) è in funzione di u, che può essere qualsiasi unità di frequenza spaziale purché sia la stessa di u(c). Prima si calcola la risoluzione limite u(c) con 1000/(0.550*f/) in l/mm. Poi si introduce u nella formula che gira intorno al rapporto u/u(c). Da lì esce MTF(u). Bisogna ricordarsi di dividere per 2 u per avere lp/mm e non l/mm, ma questo alla fine, nella formula devono essere u e u(c) espressi entrambi in l/mm o cicli/mm o cicli/pixel o anche misure angolari in radianti. Chiaramente se immetti in una calcolatrice semi-programmabile una equazione tipo MTF(u)=f(u) vai avanti e indietro fra MTF e u. Farlo a mano tutte le volte è proibitivo. Uso la SHARP EL5250, sembra che non la vendono più, deve essere una calcolatrice con il tasto MATH per andare bene.
|
| inviato il 01 Aprile 2020 ore 22:46
Grazie ancora Valgrassi , sono in debito con tutti Voi, ricordatevelo, se posso esservi utile su qualsiasi cosa ( ad es. sulle panoramiche di cui parlo nelle mie gallerie e sul mio forum "Panoramiche Monti", o su altro ), chiedete pure, sarò lieto di rendermi utile. |
| inviato il 01 Aprile 2020 ore 23:00
@Gio ti segnalo Vince Basile, nato a Kamloops in BC (Canada) e poi naturalizzatosi australiano. Non ha fatto panoramiche confrontabili con le tue ma con le varie Sony e anche un Canon 600/4 non scherza neanche lui!
flic.kr/p/2iBeyUH
Le sue foto sono scaricabili in formato originale da Flickr. È il titolare di una Technogym in sedicesimo, costruisce attrezzature per fitness. |
| inviato il 01 Aprile 2020 ore 23:22
Grazie, ho visto la panoramica con le onde del mare, è ancora più difficile da fare, le onde si muovono, mancano riferimenti per unire le foto. Idem con i laghi di montagna, l' acqua che si muove ed i riflessi variabili rendono tutto più difficile. |
| inviato il 02 Aprile 2020 ore 0:43
“ Prima si calcola la risoluzione limite u(c) con 1000/(0.550*f/) in l/mm. „
Ti ripeto la domanda, non è che la risoluzione limite ottenuta con la formula che hai indicato è in lp/mm e non in l/mm come hai scritto?
Nel sito Edmund Optics l'unità della frequenza limite è lp/mm, hanno sbagliato anche loro?
www.edmundoptics.com/knowledge-center/application-notes/imaging/diffra
|
| inviato il 02 Aprile 2020 ore 9:37
@Rolu la cosa sicura è che LW/PH è in linee/mm. Nelle mire di DPR Comparison
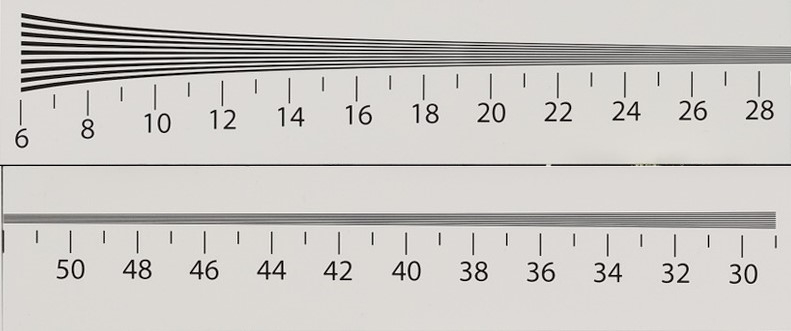
i numeri vanno moltiplicati x 100 e hai LW/PH della combinazione macchina+obiettivo che hai scelto. Queste sono a ISO 100 per la Fuji 50R. Queste mire DPR non sono molto pratiche perché non è facile stimare dove e quando le linee diventano meno o si avvitano o fanno Moiré.
Lo so che Dube e Edmund mettono sull'asse X lp/mm. Nei calcoli non succede niente se tieni fermo lp/mm o l/mm in modo consistente. In realtà l/mm non mi risultano riportate da nessuno. Formalmente si parla di "RELATIVE FREQUENCY" sulle scale X.
Appena compare "cycles" (periodo) è chiaro che è una linea bianca e una nera, cioè un intero periodo è 1 e si invoca lp/mm.
Ai nostri fini interessa mezzo periodo per soddisfare Nyquist. Se si prende la frequenza di taglio in lp/mm, tutto torna. Inconsciamente, proveniendo da digitalizzazione di segnali nel tempo, ho sempre in mente Nyquist.
Si contravviene al criterio di Nyquist se non si limita la banda con filtro AA. Con sensel sempre più piccoli si sposta Nyquist a più alte frequenze, ma non sei mai sicuro (senza AA, ma anche con AA perché non è un filtro digitale ideale, è un filtro ottico) che non oltrepassi Nyquist. Se accade ripieghi le alte frequenze verso 0 - 10 lp/mm, quelle che determinano il contrasto e secondo alcuni anche il microcontrasto. Le spurie da aliasing sono anatema perché oltre Nyquist l'MTF del sensel scende sotto MTF64. Se tutto va bene hai un'immagine più velata, che era proprio quello che si voleva evitare eliminando il filtro AA.
Ci sono finezze nella normalizzazione dell'asse X che non mi sono chiare al 100%, ci ritorno.
Dai un'occhiata anche qui:
books.google.it/books?id=57MqyPorTQMC&printsec=frontcover&dq=boreman&h |
Che cosa ne pensi di questo argomento?Vuoi dire la tua? Per partecipare alla discussione iscriviti a JuzaPhoto, è semplice e gratuito!
Non solo: iscrivendoti potrai creare una tua pagina personale, pubblicare foto, ricevere commenti e sfruttare tutte le funzionalità di JuzaPhoto. Con oltre 251000 iscritti, c'è spazio per tutti, dal principiante al professionista. |
Metti la tua pubblicità su JuzaPhoto (info) |
JuzaPhoto contiene link affiliati Amazon ed Ebay e riceve una commissione in caso di acquisto attraverso link affiliati.
