|
|
inviato il 03 Dicembre 2023 ore 9:03
È stato proposto un confronto in un altro thread dal titolo "2mpx sono abbastanza?", a pagina 2
www.juzaphoto.com/topic2.php?l=it&t=4670083&show=2
L'idea è confrontare il risultato ottenuto in due diversi modi riprendendo una determinata scena a 2Mp.
Premessa: la distanza dal soggetto rimane invariata.
Caso 1: si scatta una foto con un sensore FF da 42.2Mp (pixel pitch 4.52 micron) verso un soggetto, utilizzando un obiettivo da 500mm. Si ritaglia poi dalla foto un frame di 2Mp (sempre in formato 2:3), che racchiude la scena interessata.
Caso 2: si scatta con un sensore FF da 2Mp (pixel pitch 20.79 micron) verso lo stesso soggetto, ma questa volta utilizzando un obiettivo da 2300mm, condizione che permette di riempire l'intero sensore FF con la scena inquadrata dal ritaglio da 2Mp del caso 1.
Per cui, alla fine in entrambi i casi si ottiene una foto da 2Mp della medesima scena.
È stato supposto per semplicità che i due obiettivi presentino pari risolvenza, è stato indicato un valore di 24lp/mm proiettate da tali obiettivi sui due sensori.
Si è dibattuto su quale dei due casi offra un risultato migliore, per farlo ci si è addentrati anche nell'utilizzo delle MTF, citando la formula per cui MTF(sistema) = MTF(obiettivo) x MTF(sensore). Operare con i valori MTF non è un metodo banale, serve un minimo di conoscenza in materia per maneggiarlo.
Tale discussione non si è conclusa al termine delle 15 pagine, lo scopo di questo thread è quello di permettere a chi stava partecipando alla suddetta discussione di poter replicare agli ultimi commenti, sperando anche di riuscire a ottenere qualche risultato.
Dato lo scopo, non mi prolungo nella spiegazione di come si ottengono i valori MTF di un sensore, nota la frequenza spaziale a cui viene esposto (nella discussione si è usato il valore in lp/mm proiettato dall'obiettivo, come premesso fissato a 24). Tali spiegazioni si trovano in buona parte nel thread citato.
Per questioni di tempo, probabilmente mi limiterò a seguire gli interventi che proseguono la discussione in corso.
Qui sotto riporto l'ultimo messaggio del precedente thread. |
|
|
inviato il 03 Dicembre 2023 ore 9:07
“ @Leonardo
Le lp/mm sono in ogni caso sul piano focale. Lo stesso oggetto ripreso se con il 500mm corrisponde a 24 lp/mm, con il 2300mm corrispondera' a 24/4.6=5.2 lp/mm. E' molto probabile che l'mtf di un obiettivo a 5 lp/mm sia maggiore dell' mtf di un altro obiettivo a 24 lp/mm...
L'ovvia conclusione tecnica: bastano 2mpx purche' ci siano la focale adeguata alla foto finita che si vuole ottenere, o ancor meglio il punto di ripresa corretto „
Simone Rota, stai facendo lo stesso discorso di Rolubich, ovvero considerare un determinato valore di lp/mm nel soggetto, e di conseguenza a pari distanza maggiore è la lunghezza focale e più vengono "ingrandite" le "linee" del soggetto, che quindi sul piano focale si tramutano in meno lp/mm tanto più elevata è la lunghezza focale. Ma non è così che si definisce la risolvenza di un obiettivo, non in assoluto. Se parti da un valore di lp/mm sul soggetto, il valore che si ottiene in lp/mm sul piano focale dipende dalla distanza dal soggetto e dalla lunghezza focale. Per definire quante lp/mm un obiettivo riesce a risolvere (stabilito il valore di contrasto di soglia), si deve valutare il valore di lp/mm sul piano focale, e in questo modo se ti dico che il tal 50mm risolve 70 lp/mm con MTF50 (ad esempio al centro e a f4), mentre il tale 85mm ne risolve 75 (sempre a MTF50), allora puoi dire che l'85mm al centro ed f4 risolve più del 50mm. Se non consideri questo valore sul piano focale ottieni valori MTF non confrontabili tra lunghezze focali diverse e/o diverse distanze dal soggetto. Si può fare, alcuni grafici MTF vengono realizzati in questo modo, ma i risultati dipendono dalle condizioni del test, non sono assoluti.
Per calcolare l'MTF del sensore occorre sapere quante lp/mm sono proiettate su di esso (sul piano focale).
“ @Rolu,Leonardo è molto più semplice di come la mettete giù.
Il 2300 può risolvere tutto quello che vuole a MTF100, lo sappiamo che non è realistico, ma questo è un Gedanken Experiment. Il concetto da capire è che il collo di bottiglia è il sensore da 2 Mpx FF. Sarà capace di acquisire 24 lp/mm a MTF64 AL MASSIMO.
GAME OVER. „
Valerio, il limite del sensore in densità è quello di acquisire 24 lp/mm a MTF64, ma il suo limite generale è dato dai 2Mp... Che è lo stesso identico limite del ritaglio di 2Mp dal sensore da 42.2Mp.
Il lato lungo di un frame da 2Mp in formato 2:3 è di 1732 pixel. Questo vuol dire che, nel totale, a prescindere da quante siano le coppie di linee per millimetro proiettate, tale frame può idealmente riprodurre un linea scura ogni due pixel di larghezza, quindi 866 linee scure intervallate da altrettante linee chiare.
E il ritaglio dal sensore da 42.2Mp? Uguale, se tale ritaglio è da 2Mp il limite superiore rimane comunque di 866 coppie di linee totali. Che senso ha ragionare di quanto densamente può riprodurle se poi ignori quanto è largo il sensore?
Con 24lp/mm proiettati, un sensore FF da 2Mp ha MTF64. Nyquist a 24lp/mm. E quante coppie di linee può riprodurre in totale al massimo? 866.
Prendiamo un sensore APS-C da 2Mp (pixel pitch 13.63micron), nyquist a 36.7lp/mm, a 24lp/mm ha MTF83. Quante coppie di linee può riprodurre in totale al massimo? 866.
Un ipotetico sensore micro4/3 portato a 2:3, da 2Mp (pixel pitch 10.0 micron), nyquist a 50lp/mm, a 24lp/mm ha MTF91. Quante coppie di linee può riprodurre in totale al massimo? 866.
Sensore da 1 pollice da 2Mp (pixel pitch 7.62 micron), nyquist a 66lp/mm, a 24lp/mm ha MTF95. Quante coppie di linee può riprodurre in totale al massimo? 866.
Sensore da compatta formato 1/2.3" da 2 Mp (pixel pitch 3.56 micron), nyquist a 140lp/mm, a 24lp/mm ha MTF99. Indovina quante coppie di linee può riprodurre in totale al massimo? Sempre 866, come tutti gli altri (hanno tutti 1732 pixel sul lato lungo).
E allora come fai a dire game over?
Un altro approccio intuitivo, è ragionare all'obiettivo come "limitante" il sensore. In quale condizione il sensore riesce a riprodurre il massimo delle coppie di linee? Lo fa quando le linee sono spesse quanto i pixel, a nyquist. L'MTF è 64, sì, ma il numero di coppie di linee riprodotte è il massimo. Quindi se proietto le linee alla frequenza di nyquist sul sensore, ogni colonna di pixel può "vedere" una linea. Se il sensore è lontano da Nyquist, l'MTF sarà superiore (maggior contrasto), ma vuol dire che le linee sono più spesse di un pixel! Quindi servono più pixel per poter riprodurre una singola linea. E se siamo limitati da 1732 pixel sul lato lungo, se vengono impiegati più pixel per ogni linea significa che... possono essere riprodotte MENO coppie totali di linee. MTF maggiore, sì, ma meno dettaglio. Mi sembra davvero intuitivo.
“ Probabilmente la differenza tra me e voi è che ho fatto tante prove SIGNIFICATIVE mesi fa a cavalletto per cui è quasi sleale da parte mia arrivare al volo a certe conclusioni, come se fossi un visionario. „
Te l'ho proposto un esempio, fare una foto in DX e poi una in FX con la stessa macchina (stesso sensore), stessa lente (avente una resa abbastanza omogenea), avvicinandosi al soggetto in FX per inquadrare la stessa scena dello scatto in DX. Stessa lente e stesso sensore, quindi le lp/mm che la lente può proiettare ad un certo valore di contrasto sono le stesse (stesso MTFobiettivo), e a tale valore si calcola l'MTFsensore (uguale). Quindi MTFsistema uguale nei due casi. Qualcuno potrebbe mai pensare che la foto in DX abbia la stessa resa di quella in FX? Nessuno. Eppure, MTF uguali. Questo è un assurdo che si ottiene limitandosi a considerare solo il valore MTF.
Valerio, ho argomentato i discorsi, ho fatto esempi, se qualcosa è sbagliato si può entrare nel merito, spiegare il perchè il discorso/ragionamento/esempio è sbagliato, e così se c'è un errore viene fuori. Per te dal risultato MTF si possono trarre conclusioni sul risultato finale (la foto a 2Mp), ho spiegato perchè a me appare del tutto insensato se si ignora la dimensione del frame sul piano focale, se non mi viene spiegato perchè le mie spiegazioni sono errate la discussione si blocca (non che sia un obbligo proseguirla, ma penso che non capirsi sia una mezza sconfitta).
Per tentare un altro esempio, si può pensare ad uno scanner che deve scansionare una foto che è stampata ad un determinato valore di DPI. Diciamo 300DPI, tanto per dire un numero (è come fissare la risolvenza dell'obiettivo, l'immagine che arriva allo scanner ha una densità di dettagli fissa a 300DPI).
Quale scanner riesce ad ottenere la scansione migliore, uno che lavora a 150DPI o uno che lavora a 600DPI? Bè, se la foto a 300DPI che gli facciamo scansionare ha la stessa dimensione, lo scanner che acquisisce a 600DPI ha un netto vantaggio. Ma se nello scanner da 600DPI mettiamo una foto da 300DPI stampata a grandezza francobollo, e in quello da 150DPI la stessa foto stampata sempre a 300DPI ma a dimensione A4, scommettiamo che il risultato ottenuto dallo scanner a bassa densità è migliore?
Lo scanner da 600DPI scansiona più finemente (MTF più alto), ma scansiona finemente la dimensione di un misero francobollo. La quantità di dettagli che può rilevare è limitata dalla quantità di dettagli rappresentabili a 300DPI su un francobollo.
Così come il sensore bello denso da 42.2Mp alla fine acquisisce il frame su una piccola porzione 4.6 volte più piccola del sensore.
Mi dispiace essere molto ripetitivo, ma se non mi si spiega il perchè questi discorsi sarebbero sbagliati il massimo che posso fare è provare a riproporli diversamente.
|
|
|
inviato il 03 Dicembre 2023 ore 9:49
“ Caso 1: si scatta una foto con un sensore FF da 42.2Mp (pixel pitch 4.52 micron) verso un soggetto, utilizzando un obiettivo da 500mm. Si ritaglia poi dalla foto un frame di 2Mp (sempre in formato 2:3), che racchiude la scena interessata.
Caso 2: si scatta con un sensore FF da 2Mp (pixel pitch 20.79 micron) verso lo stesso soggetto, ma questa volta utilizzando un obiettivo da 2300mm, condizione che permette di riempire l'intero sensore FF con la scena inquadrata dal ritaglio da 2Mp del caso 1.
„
OK, anche se potevi usare due focali più umane. 
“
È stato supposto per semplicità che i due obiettivi presentino pari risolvenza „
Ok, più genericamente che abbiano curve MTF uguali.
“
è stato indicato un valore di 24lp/mm proiettate da tali obiettivi sui due sensori........(nella discussione si è usato il valore in lp/mm proiettato dall'obiettivo, come premesso fissato a 24) „
Questa è una supposizione che è in contrasto con la prima, cioè con il caso specifico delle due situazioni.
Le lp/mm proiettate dagli obiettivi che arrivano al sensore non sono le stesse nei due casi, non capisco perchè le devi fissare a priori.
Stessa identica assunzione errata che hai fatto nell'ultimo messaggio dell'altra discussione
“ Te l'ho proposto un esempio, fare una foto in DX e poi una in FX con la stessa macchina (stesso sensore), stessa lente (avente una resa abbastanza omogenea), avvicinandosi al soggetto in FX per inquadrare la stessa scena dello scatto in DX. Stessa lente e stesso sensore, quindi le lp/mm che la lente può proiettare ad un certo valore di contrasto sono le stesse (stesso MTFobiettivo) , e a tale valore si calcola l'MTFsensore (uguale). Quindi MTFsistema uguale nei due casi. Qualcuno potrebbe mai pensare che la foto in DX abbia la stessa resa di quella in FX? Nessuno. Eppure, MTF uguali. Questo è un assurdo che si ottiene limitandosi a considerare solo il valore MTF. „
Consideri le lp/mm che l'obiettivo può proiettare e non quelle che effettivamente proietta.
Se con il FX ti avvicini fino ad avere le stessa inquadratura le lp/mm da usare sono 1.5 volte inferiori.
Non c'è nessun risultato assurdo ed i valori MTF sono adatti a determinare la qualità dell'immagine (solo dal punto di vista del contrasto), c'è solo da tenere conto di questa grande verità:
nonsense in ----> nonsense out
o nella sua versione più rude:
s**t in ----> s**t out
|
|
|
inviato il 03 Dicembre 2023 ore 11:19
Amici miei, devo fare i pizzoccheri e sono indietro. L'operazione più lenta è grattare tre tipi di formaggio a mano.
In ogni caso vi risponderò perché abbiamo spezzato le reni al Frosinone, altrimenti mi ritiravo nel lutto più stretto.
Dico subito che ho a disposizione una Nikon D40 che è 6 Mpx CCD, non 2 Mpx FF. Sto pensando ad una prova a cavalletto SIGNIFICATIVA, ma non è banale, ci vorrebbe davvero una 2 Mpx FF.
Reitero che per me la fotografia non sono i logaritmi o le FFT.
Non nascondo che chi non sa calcolarsi un log2 non mi colpisce per la sua perspicacia matematica.
Limite mio, lo riconosco, magari lo gnorri è un eminente critico, tipo Smargiassi, che capisco a corrente alternata.
|
|
|
inviato il 03 Dicembre 2023 ore 11:23
Simone Rota, stai facendo lo stesso discorso di Rolubich, ovvero considerare un determinato valore di lp/mm nel soggetto, e di conseguenza a pari distanza maggiore è la lunghezza focale e più vengono "ingrandite" le "linee" del soggetto, che quindi sul piano focale si tramutano in meno lp/mm tanto più elevata è la lunghezza focale.
****************
Esatto, sostanzialmente mi pare tu abbia capito
Ma non è così che si definisce la risolvenza di un obiettivo, non in assoluto.
*****************
Anche questa affermazione e' vera..ma molto meno importante ai fini del risultato.
Dovendo riprendere un soggetto lontano e potendo scegliere tra un grandangolare ed un teleobiettivo, tutti i fotografi prenderanno il secondo.
Avendo invece 2 teleobiettivi di pari lunghezza focale, sara' utile prendere quello piu' risolvente |
|
|
inviato il 03 Dicembre 2023 ore 14:28
Nell'altro 3d Paolo aveva subito notato che un obiettiva 2300 mm non si dà, quindi erano discussioni sul sesso degli angeli. Giusto.
Adesso, dopo avere riaffermato che sono uno sperimentale e non un teorico, la palla ce l'ho in mano io e per ora non ho trovato una prova SIGNIFICATIVA
I pizzoccheri sono venuti bene! |
|
|
inviato il 03 Dicembre 2023 ore 21:56
“ ...la stessa che, da ragazza, mia madre pronunciava con sufficienza dopo aver letto la pagella con la quale collezionavo solo voti alti, al netto della matematica, la mia bestia nera. „
Anyone? |
|
|
inviato il 03 Dicembre 2023 ore 23:27
Non sembrano esserci FF con 2 Mpx (et pour cause!). Proviamo e mettere giù qualche considerazione lo stesso.
La relazione di base diventa:
MTF(sistema)=MTF(ottica)*MTF(sensore)*MTF(filtro AA) (1)
Sappiamo che MTF va da 0 a 1, oppure da 0 a 100 in %. L'aggiunta di MTF(filtro AA) abbassa quindi la MTF(sistema).
Il filtro AA (anche: OpticalLowPassFilter, OLPF) è obbligatorio perché con Nyquist a 24 lp/mm sarebbe un disastro senza. Ci sarebbe "aliasing" perché è quasi impossibile che un'ottica faccia arrivare sempre meno di 24 lp/mm al sensore.
Abbiamo un dato certo per iniziare: il sensore 2 Mpx FF ha Nyquist a 24 lp/mm.
Con l'aggiunta del filtro AA da 24 lp/mm si può ipotizzare una diminuzione (poniamo) a 22 lp/mm.
Passare da Nyquist a 24 lp/mm a 22 lp/mm ha un effetto positivo su MTF(sensore), cambia da MTF(64) a MTF(69).
Decisivo: acquisendo frequenze spaziali decrescenti, cresce MTF(sensore) finché con tutto bianco o tutto nero si avrebbe frequenza spaziale nulla e MTF100. Evitare di pensare che il sensore acquisisca sempre a Nyquist o alla frequenza spaziale massima di 22 lp/mm, perché non è vero.
L'ipotetico tele da 2300 mm (teniamo buona la foto balneare di Otto72) invierà anche frequenze spaziali alte al sensore che verranno tagliate PERFETTAMENTE (perché il sensore è virtuale!) dal filtro AA passa basso.
Al sensore arriveranno al massimo 22 lp/mm con MTF(69), ma è decisivo capire che non tutti i pixel porteranno informazione delle frequenza massima possibile (non dimentichiamoci che quella delle 22 lp/mm è un'assunzione, anche se verosimile).
Se tutto questo non è chiaro, tanto vale mollare la descrizione secondo MTF e introdurre astruse (nel senso che IO non le afferro) considerazioni come nel 3d precedente. Quindi: una necessaria pausa di riflessione. |
|
|
inviato il 04 Dicembre 2023 ore 7:30
“ OK, anche se potevi usare due focali più umane. MrGreen „
Hahaha sì bè si era partiti dalla foto staccata a 500mm con la a7R3, quindi poi per inquadrare il ritaglio di quei fatidici 2Mp la focale necessaria risultava 2300mm. Ho citato quelle focali solo per attenermi all'esempio originale, tanto è un esercizio concettuale =)
“ Ok, più genericamente che abbiano curve MTF uguali. „
Perfetto.
“ Questa è una supposizione che è in contrasto con la prima, cioè con il caso specifico delle due situazioni.
Le lp/mm proiettate dagli obiettivi che arrivano al sensore non sono le stesse nei due casi, non capisco perchè le devi fissare a priori.
Stessa identica assunzione errata che hai fatto nell'ultimo messaggio dell'altra discussione „
Appare errata perchè secondo me non viene presa per quel che intende rappresentare, bisogna capire qual'è il significato di quelle 24lp/mm.
Si voleva tradurre con dei valori il fatto che i due obiettivi hanno stessa risolvenza (stesse curve MTF come specifichi tu), per poter procedere a dei calcoli.
Se inquadriamo un pattern che ha una sua frequenza spaziale (è una rappresentazione di dettaglio ad una specifica frequenza), la proiezione di tale pattern sul piano focale ovviamente cambia se a pari distanza cambia la focale. La frequenza spaziale originaria del pattern rimarrebbe identica sul piano focale se l'obiettivo stesse lavorando con rapporto di riproduzione 1:1 (ingrandimento macro 1X se vogliamo), più cala il rapporto di riproduzione, più il pattern è "rimpicciolito" sul piano focale rispetto alla realtà, e più quindi ne aumenta la frequenza spaziale. A pari distanza, un obiettivo con lunghezza focale maggiore ha un rapporto di riproduzione superiore, e quindi la frequenza spaziale che proietta (partendo da quel particolare pattern) è minore (rispetto ad obiettivi di lunghezza focale inferiore). Ora, tutto questo discorso si fonda sull'idea di inquadrare un particolare pattern, che simula dettagli ad una specifica frequenza spaziale. Nella realtà, ogni scena presenta una disomogenea distribuzione di dettaglio, e il particolare dettaglio che ad una certa distanza pare presentarsi con una determinata frequenza spaziale, se osservato da più vicino, o, esagero, al microscopio, svela dettagli ad una frequenza molto superiore. La realtà non è un pattern, è questo il punto. L'uso di pattern ben contrastati ad una data frequenza (o frequenze variabili) è solo uno strumento utile a rilevare le capacità di un obiettivo di proiettare l'immagine di tale pattern mantenendone il contrasto più o meno elevato.
Come si può fare a qualificare questa capacità di un obiettivo?
Per prima cosa, per avere risultati di validità generale, si sposta l'attenzione dalla frequenza spaziale sulla scena inquadrata alla frequenza spaziale proiettata sul piano focale, in questo modo ci si svincola dalle condizioni di ripresa, si analizza il risultato sul formato, così facendo si definisce una capacità dello strumento sul proprio formato e sarà chi fa utilizzo di tale strumento a regolarsi di conseguenza per gli impieghi specifici da affrontare. Questo si può fare in modi più o meno complessi, un modo semplice è avere una stampa con tante coppie di linee ben contrastate, inquadrare tali linee da distanze diverse ne modifica la frequenza spaziale sul piano focale, e così quella stessa sequenza di linee la si può inquadrare a 5lp/mm, 10, 20, 30... Eccetera (frequenze sul piano focale). Per ognuna di queste frequenze si può rilevare il contrasto che presentano, eventualmente in punti diversi della proiezione (dal centro al bordo) e alle diverse aperture dell'obiettivo. Così si può costruire un grafico MTF di tale obiettivo (non complichiamo il discorso riguardo la resa rispetto a linee sagittali e meridionali, per ogni combinazione si può rilevare il contrasto).
Da qui, possiamo dire che un obiettivo ha MTF80 a tot lp/mm, MTF 60 a tot lp/mm, e così via. Questi sono risultati assoluti, poichè riferiti al piano focale, dopo di che il fotografo sa che se lavora a 1:1 i dettagli a X lp/mm DEL SOGGETTO arriveranno sul sensore al valore di contrasto indicato dal corrispondente valore MTF di X lp/mm, se lavora a 1:10 invece dovrà riferirsi al valore MTF di 10X lp/mm, e via dicendo. Se si qualifica un obiettivo in questo modo (non sempre i grafici MTF sono riportati a queste condizioni) allora è facile confrontare obiettivi diversi tra loro (diverso formato e/o lunghezza focale), valori MTF superiori corrispondono a capacità di risolvenza superiori. Si può iniziare a parlare del fatto che una lente sia ad esempio "più nitida" rispetto ad un'altra, dopo di che è ovvio che la lunghezza focale e la distanza dal soggetto influiscono sulla capacità di riprodurre un determinato dettaglio, ma le specifiche ottenute come sopra sono assolute, rappresentano qualità ottiche dell'obiettivo, il risultato finale dipenderà ovviamente dall'utilizzo che il fotografo ne fa.
Quindi, come la definiamo questa capacità di risolvenza di un obiettivo? Di solito si considera un livello di contrasto del 50% al centro, quindi MTF50, per rappresentare la suddetta capacità si prende il valore in lp/mm (sul piano focale) a cui il centro dell'obiettivo presenta MTF50. Così puoi dire che il tale obiettivo a f4 riesce a risolvere 40lp/mm (MTF50) e il tal altro obiettivo riesce a risolverne 55. Nessuno vieta di considerare tali valori ad un livello di contrasto differente, 50% è solo il valore più utilizzato (ed ha abbastanza senso).
Nella famosa formula per ricavare l'MTF del sistema, il valore MTF del sensore viene calcolato a partire da una determinata frequenza spaziale che deve rilevare (quindi anche qui ovviamente sul piano focale). Serve quindi un valore. Valgrassi ha suggerito 24lp/mm, poichè a tale valore il sensore FF da 2Mp si trova a nyquist. Dire che i due obiettivi permettono la stessa risolvenza (pari qualità ottica in risolvenza), significa che a 24lp/mm (piano focale) il loro MTF è il medesimo. Che sia MTF50 o MTF80, poco ci importa, è uguale, ma si ricava l'MTF del sensore a 24lp/mm.
Tutto questo permette di ottenere valori assoluti, in riferimento alle capacità di ogni combinazione sensore + obiettivo di poter registrare densità di dettaglio. È una densità, è come se ci si stesse riferendo "ad ogni mm" di immagine sul piano focale.
Il fatto di considerare che lo stesso soggetto è riprodotto ad una dimensione differente sui due sensori, e che quindi la stessa frequenza spaziale sul soggetto viene riportata in modo differente sui piani focali dei due obiettivi a lunghezza focale diversa, toglie assolutezza ai risultati delle MTF. Considerare quelle 24lp/mm (ad un dato valore MTF) permette di ricavare l'MTF totale effettivo dei due sistemi (con tutte le premesse fatte). È una misura di qualità, una grandezza intensiva. Se vogliamo valutare il risultato che si ottiene catturando una certa scena, il fatto che lo stesso soggetto (e quindi l'intera scena stessa) sia riprodotta a grandezza differente sui due sensori trova considerazione nel momento in cui combiniamo il valore MTF (assoluto) dei due sistemi con la dimensione dell'immagine riprodotta nei due sistemi. Nello specifico un'immagine risulta larga 36mm e l'altra 7.8mm .
È più chiaro il senso di considerare lo stesso valore in lp/mm per definire due obiettivi parimenti risolventi?
Ci si svincola dalla scena, considerare tot lp/mm del soggetto crea un po' di confusione, le lp/mm sono uno strumento utile per effettuare misurazioni, come si associano le lp/mm ad un soggetto che non sia un pattern?
Definendo la capacità di risolvenza di un obiettivo come sopra (e normalmente viene fatto così...), si va' a considerare la "bontà" del sistema (e per la bontà del risultato si tiene conto anche della dimensione dell'immagine proiettata nel sistema).
“ Consideri le lp/mm che l'obiettivo può proiettare e non quelle che effettivamente proietta. „
Considero il dato in lp/mm della risolvenza dell'obiettivo, le lp/mm che effettivamente proietta non so cosa voglia dire, si sta inquadrando una scena reale non un cartellone con un pattern.
“ Se con il FX ti avvicini fino ad avere le stessa inquadratura le lp/mm da usare sono 1.5 volte inferiori.
Non c'è nessun risultato assurdo ed i valori MTF sono adatti a determinare la qualità dell'immagine (solo dal punto di vista del contrasto), c'è solo da tenere conto di questa grande verità:
nonsense in ----> nonsense out
o nella sua versione più rude:
s**t in ----> s**t out „
Come ho accennato a inizio commento, il punto è capirsi su cosa si sta dicendo. Il significato che abbiamo dato a quei valori in lp/mm, è evidentemente diverso.
Lo stesso obiettivo (stesse curve MTF), se lo uso per inquadrare la stessa scena con sensori di dimensioni diverse, sul piano focale offrirà le stesse identiche prestazioni. La qualità ottica è la stessa (a meno del fatto che il punto di fuoco cambia, e che la resa sui bordi cala). Il fatto che usarlo con sensore più grande dia un risultato migliore, deriva dal fatto che sul sensore più grande viene proiettata un'immagine... più grande. La stessa qualità ottica ma applicata su una superficie maggiore. Se la scena inquadrata è la stessa, proiettarla più in grande permette una rappresentazione più dettagliata.
“ Non c'è nessun risultato assurdo ed i valori MTF sono adatti a determinare la qualità dell'immagine „
Per rendere i valori MTF adatti a determinare direttamente la qualità dell'immagine finale devi creare delle specie di equivalenze, modificare i valori in lp/mm in funzione al formato (o alla lunghezza focale, discorso analogo), lo puoi anche fare ma non è quel che stavo facendo (e che mi pare stesse facendo anche Valgrassi), la qualità finale dell'immagine l'ho valutata considerandone anche la dimensione, i valori MTF che ho usato sono relativi all'obiettivo, al sensore, e poi alla loro combinazione, a prescindere dal formato: in questo senso dico che sono valori assoluti.
È come dire che due stampanti/scanner lavorano a tot DPI, se poi stampi/scansioni a dimensioni differenti è ovvio che ne tieni conto, ma l'indicatore qualitativo espresso in DPI (analogo al valore MTF) rimane quello. Se lo trasformi per ottenere una sorta di equivalenza su formati diversi lo puoi fare, è un modo diverso da quel che ho fatto io, parlando di risolvenza uguale tra due lenti io ho considerato due valori uguali (ripeto, quando si misura la risolvenza in lp/mm di un obiettivo lo si fa riferendosi ad un certo di valore di contrasto e AD UN MILLIMETRO SUL PIANO FOCALE, quindi in modo del tutto indipendente da lunghezza focale e formato, rappresenta una qualità ottica, non dell'intera immagine che esce dall'obiettivo).
Se hai letto tutto questo, mi auguro che ci siamo chiariti su quale sia il significato di quel valore "24lp/mm" e che non consideri più quel che ho detto in precedenza come "nonsense" =)
Se si interpreta lo stesso dato con due significati diversi è facile non trovare senso in un discorso.
Valerio come è andata la tua battaglia con il formaggio?  chi ha vinto? chi ha vinto?
Appena riesco rileggo tutto e rispondo anche a te e Simone Rota  (come dicevo non ero sicuro di avere il tempo per dedicarmi pienamente ad un nuovo thread). (come dicevo non ero sicuro di avere il tempo per dedicarmi pienamente ad un nuovo thread).
Intanto buona giornata! |
|
|
inviato il 04 Dicembre 2023 ore 8:43
“ Se hai letto tutto questo, „
Sì, ma con una grande difficoltà perchè, secondo me, fai le cose molto più complicate di quello che sono.
La formula MTF(sistema)=MTF(sensore)*MTF(ottica) è comodissima perchè separa le due componenti che possono essere calcolate separatamente, senza che una influenzi l'altra.
Le lp/mm da prendere in considerazione sono quelle che arrivano al sensore, cioè immagina di essere dentro la fotocamera, vedere l'immagine formata sul sensore/pellicola, e contare quante copie di linee ci sono in un millimetro; se sai la focale, la distanza e la frequenza della scena le puoi calcolare invece di contarle.
Una volta misurate o calcolate le lp/mm da prendere in considerazione, MTF(sensore) si calcola e MTF(obiettivo) devi misurarlo con prove su banco ottico.
Fai la moltiplicazione ed ottieni MTF(sistema).
Non c'è molto alto da dire.
|
|
|
inviato il 04 Dicembre 2023 ore 8:47
@Leonardo tu giustamente lavori, invece io sono un dipendente di Vincenzo Caridi che non esige niente da me, anzi, mi mantiene a 76 anni compiuti in luglio.
Leggerò oggi molto attentamente questo tuo ultimo intervento.
La relazione (1) che ho riportato prescinde da MTF schermi, stampe, visione umana, distanza di osservazione e tutto quello che merita una quantifica. In sostanza siamo di fronte a una produttoria estesa a seconda dei bisogni basata su MTF. Sono convoluzioni (operazione non immediata sotto integrale) che attraverso FT diventano prodotti fattorizzati.
I fotografi non devono allarmarsi, c'è chi al mondo sa calcolarsi le FT di ogni passaggio MTF.
Noi dobbiamo solo capire i risultati finali delle convoluzioni via MTF, per fortuna.
Riporto questa MTF per chiarire cosa fa un filtro AA. Ci sono buone ragioni teoriche (criterio di Nyquist) per usare SEMPRE un filtro AA, farlo capire a un fotografo medio è quasi impossibile perché è convinto che senza filtro AA è tutto meglio. In realtà è il contrario, diciamo che percettivamente non è facile accorgersi del male che ti fa la mancanza di un filtro AA (OLPF). Vale sempre "ignorance is bliss" in casi come questi.
Oppure La Palice sotto forma di "quello che conta è l'immagine finale soltanto": uno poi si chiede perché fotografi con queste convinzioni leggano 3d di teoria della fotografia digitale, il più delle volte senza capirci tanto.
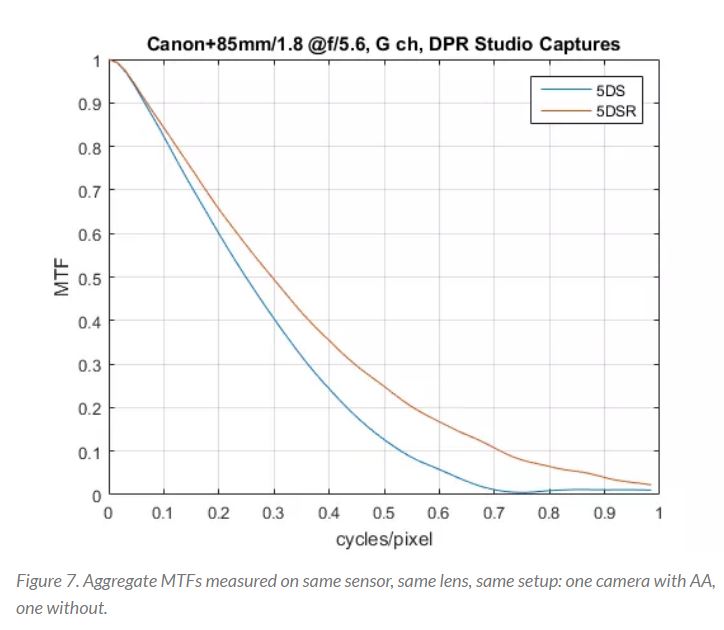
Anni fa Canon introdusse due 5DS. Una aveva filtro AA (5DS), l'altra aveva il filtro AA neutralizzato da un secondo filtro in contrfase (5DSR). La 5DSR non è una macchina senza filtro AA, ne ha addirittura due di filtri per emulare una macchina senza filtro AA.
cycles/pixel sta per coppie di linee, linea bianca + linea nera è un ciclo completo.
Nyquist per definizione è a 1/2=0.5 cycles/pixel. Intuitivamente Nyquist si assicura che in un pixel NON siano rappresentate insieme due linee (metti: una bianca e una nera insieme), perché allora perdiamo risoluzione, non le distinguiamo.
A Nyquist la 5DS ha MTF12 (traccia blu). Rigorosamente si definicono risolte due linee almeno con MTF9, ma anche MTF12 sta a significare che l'occhio non lo percepisce (grigiastro).
A Nyquist la 5DSR ha MTF25, percepibile e come!
Un requisito di Nyquist è che la banda passante sia limitata, la 5DSR arriva a MTF10 con 0.7 cicli/pixel , in altre parole lascia passare artefatti.
Un inciso. La 5DSR costava ~ €500 in più della 5DS perché aveva due filtri AA in opposizione di fase.
Per cui molti hanno scelto la 5DS per motivi economici. Escluso che sapessero degli artefatti della 5DSR.
Lo stesso vale per chi ha scelto la 5DSR in buona fede.
Se uno non ha basi solide sulla acquisizione di segnali, continua a pensare che la 5DSR sia meglio (?).
Va detto che si può fotografare bene anche senza capire più che tanto della teoria (che poi alla fine è pratica, non fumisteria).
Questo grafico ha poco in comune con le MTF disponibili in rete, dove un fotografo va a vedere l'uniformità di un obiettivo dal centro ai bordi, di solito a TA. TA vuole dire diffrazione al minimo.
Sigma cita MTF a 10 e 30 lp/mm specificando "teoriche" e misurando con la "diffrazione". Naturalmente a TA non c'è quasi differenza, la differenza sarebbe netta a f/16 dove la diffrazione ha più peso.
Se uno divide punto a punto le due curve del grafico gli esce una campana cosinusoidale del filtro AA.
Dopo la MTF del sensore che è una semplice sinc(x), anche qui abbiamo un cos(x) facilmente calcolabile che è una MTF.
A chi interessa basta andare a vedere dove la traccia blu va a MTF0 (ossia quando l'angolo è pi_greco/2), da lì si risale alla forma della cosinusoide.
|
|
|
inviato il 04 Dicembre 2023 ore 10:06
“ La realtà non è un pattern, è questo il punto. „
La realtà non è un pattern, ma questo non cambia le cose.
La realtà è un insieme di frequenze e contrasti diversi ma:
- le curve MTF degli obiettivi si possono misurare per ogni frequenza ed il valore MTF del sensore è noto per ogni frequenza, quindi per tutte le frequenze esistenti nella scena;
- qualsiasi sia il contrasto della scena reale le formule sono valide (il fatto che le mire ottiche siano generalmente bianche e nere, quindi con contrasto alto e non come la realtà, non cambia niente) perchè forniscono la percentuale di contrasto restituito che si può applicare per ogni contrasto iniziale sia presente nella scena reale.
C'è tutto quello che serve, non c'è bisogno di altro.
|
|
|
inviato il 04 Dicembre 2023 ore 15:54
“ Dovendo riprendere un soggetto lontano e potendo scegliere tra un grandangolare ed un teleobiettivo, tutti i fotografi prenderanno il secondo.
Avendo invece 2 teleobiettivi di pari lunghezza focale, sara' utile prendere quello piu' risolvente „
Certo Simone.
Diciamo che in questo esempio c'è la variabile in più della densità del sensore. Quindi capire cosa sia preferibile tra focale più corta e sensore molto denso (con ritaglio), o focale più lunga e sensore meno denso, considerando la stessa risoluzione finale e obiettivi di pari risolvenza. Dal punto di vista dell'SNR vince sicuramente il sensore meno denso (sfrutta una superficie maggiore, non necessitando il ritaglio), dal punto di vista del dettaglio secondo me anche, e di questo si dibatte  (ribadendo il fatto che l'ipotesi della pari risolvenza è poco equa, perchè ottenere una lunghezza focale più lunga allo stesso livello di risolvenza è molto più costoso). (ribadendo il fatto che l'ipotesi della pari risolvenza è poco equa, perchè ottenere una lunghezza focale più lunga allo stesso livello di risolvenza è molto più costoso).
“ Dico subito che ho a disposizione una Nikon D40 che è 6 Mpx CCD, non 2 Mpx FF. Sto pensando ad una prova a cavalletto SIGNIFICATIVA, ma non è banale, ci vorrebbe davvero una 2 Mpx FF. „
La D40 ha un pixel Pitch di 7.88 micron, quindi la stessa densità di un sensore FF da 14Mp circa. Serve una differenza non troppo piccola, quindi magari un sensore APS-C intorno a 24Mp almeno (o FF con una cinquantina...). In modo che le lunghezze focali siano almeno una il doppio dell'altra. Con cosa potresti confrontare di più denso?
Il limite più grande secondo me è riuscire a trovare i due obiettivi, con lunghezza focale molto distante e stessa capacità risolvente.
“ Le lp/mm da prendere in considerazione sono quelle che arrivano al sensore, cioè immagina di essere dentro la fotocamera, vedere l'immagine formata sul sensore/pellicola, e contare quante copie di linee ci sono in un millimetro; se sai la focale, la distanza e la frequenza della scena le puoi calcolare invece di contarle.
Una volta misurate o calcolate le lp/mm da prendere in considerazione, MTF(sensore) si calcola e MTF(obiettivo) devi misurarlo con prove su banco ottico.
Fai la moltiplicazione ed ottieni MTF(sistema).
Non c'è molto alto da dire. „
Certo, fare il calcolo da lp/mm del soggetto a lp/mm sul piano focale è facile (note distanza e lunghezza focale). Quindi quante lp/mm arrivano dalla scena? Nell'altro thread c'è la foto, quante lp/mm ci sono nei soggetti?  come fai a definirlo? Io capisco il senso del distinguere le linee MTF in diversi valori di lp/mm, per distinguere la resa dell'obiettivo davanti a scene più o meno ricche di dettagli rilevanti, ma come fai a definirne un numero? Quante lp/mm associ ad un pino? Quante invece ad una montagna? Mi sembra un po' assurdo come approccio, esistono criteri in questo senso? come fai a definirlo? Io capisco il senso del distinguere le linee MTF in diversi valori di lp/mm, per distinguere la resa dell'obiettivo davanti a scene più o meno ricche di dettagli rilevanti, ma come fai a definirne un numero? Quante lp/mm associ ad un pino? Quante invece ad una montagna? Mi sembra un po' assurdo come approccio, esistono criteri in questo senso?
E se definiamo questo valore, calcolando i corrispondenti valori di lp/mm sul piano focale dei due obiettivi, quali valori MTF (diversi) associamo mantenendo l'ipotesi che i due obiettivi abbiano le stesse curve?
Dici che rendo le cose più complicate di quello che sono, ma nel mio esempio ho tradotto le 24lp/mm suggerite da Valgrassi con due valori MTF uguali per i due obiettivi, facendo i calcoli per le 24lp/mm, è più complicato questo rispetto al dover valutare quante lp/mm ci sono nella scena (e sul serio non capisco come si faccia...), calcolare le corrispondenti sul piano focale ed andare a cercare il valore MTF per QUELLE particolari frequenze?
A me sembra un po' un casino.
“ - le curve MTF degli obiettivi si possono misurare per ogni frequenza ed il valore MTF del sensore è noto per ogni frequenza, quindi per tutte le frequenze esistenti nella scena;
...
C'è tutto quello che serve, non c'è bisogno di altro. „
Quindi quali valori prendiamo? Quante lp/mm arrivano al 500mm e al 2300mm? I valori MTF da dove li prendiamo?
(Scusami la provocazione, è in tono soft... È che non capisco dove si arriva) |
|
|
inviato il 04 Dicembre 2023 ore 16:23
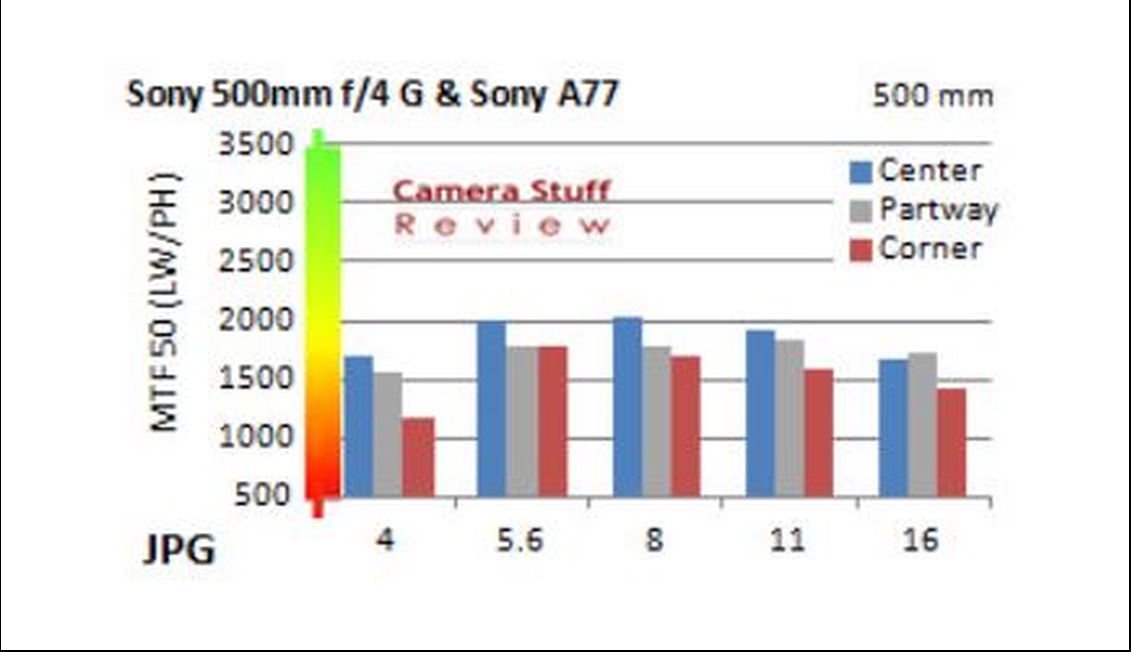
Trovati i dati MTF del 500 mm di Otto72 (dove sei?)!
Decifriamo questi dati.
La macchina è una Sony A77 aps-C con 15.6 mm di lato corto.
Da f/5.6 a f/8 esibisce il valore ~ 2000 a MTF50.
Per trovare le lp/mm si divide 2000 per 2 e per 15.6mm.
Escono 64 lp/mm a MTF50, non male, ma certamente un Canon 500 mm f/4 farebbe di meglio.
|
|
|
inviato il 04 Dicembre 2023 ore 16:49
“ Quante lp/mm associ ad un pino? Quante invece ad una montagna? Mi sembra un po' assurdo come approccio, esistono criteri in questo senso? „
“ dover valutare quante lp/mm ci sono nella scena (e sul serio non capisco come si faccia...) „
nella scena ripresa ci saranno dei particolari che hanno una certa dimensione. Non importa quale sia questa dimensione, importa solo che siano esattamente gli stessi ad essere fotografati con i due sistemi che si vogliono confrontare dalla stessa distanza.
Il rapporto tra le focali usate determina il rapporto tra la dimensioni di questi stessi particolari riprodotti sul sensore.
Il pixel pitch del sensore cambia il limite di registrazione (Nyquist) dei particolari dello spazio oggetto ma una volta fissata la focale, essendo Nyquist individuabile a livello di sensore.
Si può riscontrare aliasing con particolari molto fini e ripetitivi. Se però ci si avvicina o/e si utilizza una focale molto lunga questi stessi particolari non sono più cosi fini...ovvio, no ?
EDIT: vedo che nemmeno ci fossimo messi d'accordo nel messaggio successivo Valgrassi ha messo un esempio di quanto detto sopra |
Che cosa ne pensi di questo argomento?
Vuoi dire la tua? Per partecipare alla discussione iscriviti a JuzaPhoto, è semplice e gratuito!
Non solo: iscrivendoti potrai creare una tua pagina personale, pubblicare foto, ricevere commenti e sfruttare tutte le funzionalità di JuzaPhoto.
Con oltre 257000 iscritti, c'è spazio per tutti, dal principiante al professionista. |

Metti la tua pubblicità su JuzaPhoto (info) |


 JuzaPhoto contiene link affiliati Amazon ed Ebay e riceve una commissione in caso di acquisto attraverso link affiliati.
JuzaPhoto contiene link affiliati Amazon ed Ebay e riceve una commissione in caso di acquisto attraverso link affiliati.